

Next: About this document ...
Up: Cercle de Mohr des
Previous: 1 Rappels sur la
Subsections
Soient 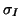 et
et 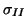 (
(
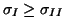 )les
contraintes principales,
)les
contraintes principales,
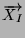 et
et
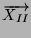 les vecteurs propres associés, alors pour toute orientation de facette
les vecteurs propres associés, alors pour toute orientation de facette
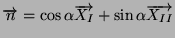 la contrainte normale
la contrainte normale 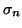 et la contrainte tangentielle
et la contrainte tangentielle
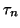 se trouvent sur un cercle appelé cercle de Mohr.
se trouvent sur un cercle appelé cercle de Mohr.
- Le centre du cercle C est situé sur l'axe des contraintes normales
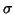 à l'abscisse
à l'abscisse
- On peut tracer le cercle si on connaît un point quelconque du cercle,
c'est à dire la contrainte normale et la contrainte tangentielle pour
une normale particulière.
- La contrainte tangentielle maximale est
- Les angles partant du centre du cercle de Mohr sont égaux aux angles
réels multipliés par -2.
On donne :
avec 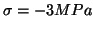 et
et 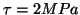
- Tracer le cercle de Mohr
- Calculer les contraintes principales et indiquer les orientation des
directions principales de la contrainte.
- Calculer la valeur de la contrainte de cisaillement maximale et l'orientation
de la facette correspondante.
- Trouver la contrainte normale et la contrainte tangentielle pour une
facette orientée par le vecteur
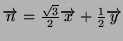
Résolution:
- Le centre du cercle est à un point d'abscisse
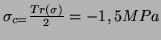
Pour une facette orientée par le vecteur
 on a :
on a : 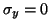 et
et
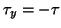
On peut donc tracer le cercle:
- Le rayon du cercle est
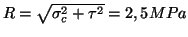 et
et
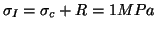 ,
,
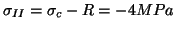
Sur le cercle de Mohr, l'angle entre
 et
et
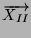 est
est
L'angle entre
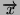 et
et
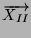 est dans la réalité :
est dans la réalité :
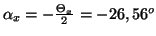
- La contrainte de cisaillement maximale est
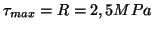 ,
elle est obtenue pour une facette orientée par le vecteur
,
elle est obtenue pour une facette orientée par le vecteur
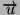 tel que l'angle entre
tel que l'angle entre
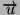 et
et
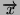 soit
soit 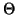 sur le cercle de Mohr avec
sur le cercle de Mohr avec
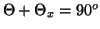 soit
soit
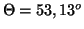
l'angle entre
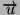 et
et
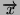 est dans la réalité :
est dans la réalité :
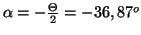
- L'angle entre
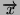 et
et
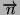 est
dans la réalité:
est
dans la réalité:
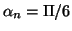 , sur le cercle de Mohr,
on a
, sur le cercle de Mohr,
on a
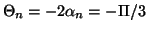 .
.
Si on pose:
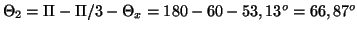 ,
on a :
,
on a :
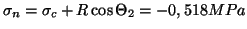 et
et
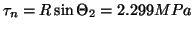


Next: About this document ...
Up: Cercle de Mohr des
Previous: 1 Rappels sur la
La Borderie
2002-09-25
![]() et
et ![]() (
(
![]() )les
contraintes principales,
)les
contraintes principales,
![]() et
et
![]() les vecteurs propres associés, alors pour toute orientation de facette
les vecteurs propres associés, alors pour toute orientation de facette
![]() la contrainte normale
la contrainte normale ![]() et la contrainte tangentielle
et la contrainte tangentielle
![]() se trouvent sur un cercle appelé cercle de Mohr.
se trouvent sur un cercle appelé cercle de Mohr.
![\begin{displaymath}
\overline{\overline{\sigma }}\left[ \begin{array}{cc}
\sigma...
...\right] _{\left( \overrightarrow{x},\overrightarrow{y}\right) }\end{displaymath}](img46.png)